This page is a one-stop shop for all your finding area and circumference of a circle exercises. Catering to the learning needs of students in grade 5 through grade 8, these printable worksheets practice the topic pretty much across the board: easy, moderate and hard. The job in the easy set is to calculate the area and circumference of the circles with radius ranging from 1 to 25. The moderate set requires rounding answers to tenth place with the radius of circles ranging between 25 and 100. In the hard worksheets, the radius is rendered in decimal and the task is to round your answers to two decimal places. Use pi = 3.14 wherever necessary. Explore some of these worksheets for free!
Select the Measurement Units U.S. Customary Units Metric Units
Applying the formula, Area = pi * r 2 , find the area of each circle.
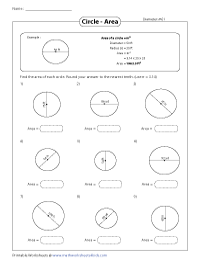
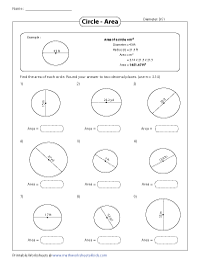
Find the radius from diameter and apply the formula to find the area of a circle.



Each printable worksheet has 9 problems on finding area of a circle with the known radius or diameter. Two simple word problems and one story problem included.
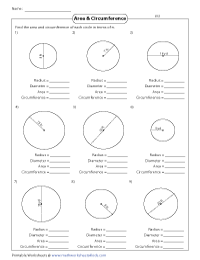
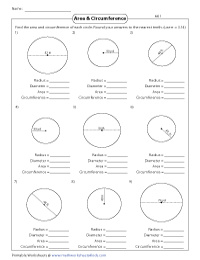
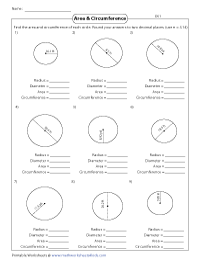
These are the perfect review worksheets in finding both area and circumference of the circle.

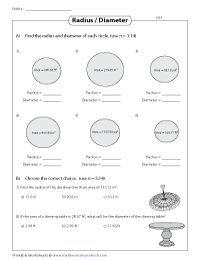
Dividing the area by pi or 3.14, you get r 2 . Taking the square root, you get radius. Solve each problem based on this technique.



Find the area from the circumference of each circle in this stock of worksheets for 7th grade students. Word problems included to understand real-life application.
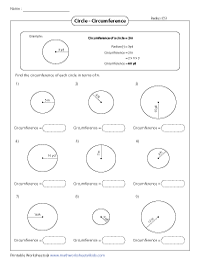
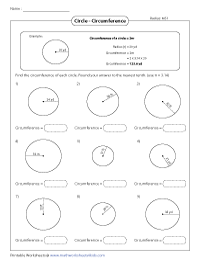
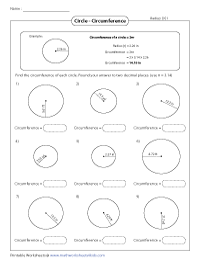
Applying the formula, Circumference = 2 * pi * r, find the circumference of each circle.
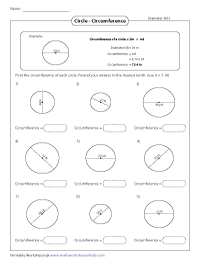 Circumference from Diameter - Moderate" width="190" height="250" />
Circumference from Diameter - Moderate" width="190" height="250" />
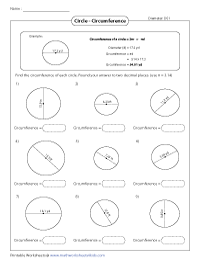 Circumference from Diameter - Difficult" width="190" height="250" />
Circumference from Diameter - Difficult" width="190" height="250" />
To find the circumference, multiply diameter with pi value. Each pdf worksheet has 9 problems.

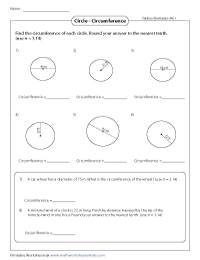
Circumference of a circle worksheet contains six standard problems and two word problems.


Divide the circumference by pi or 3.14. You get the diameter. Answer the questions.



Each worksheet has 8 problems finding circumference from area of a circle. Simple word problems included.
Imagine two circles with different radii, but the same center; can you calculate the area of the region in between? Scout around these pdf worksheets, pore over the examples, and solve similar problems on area of an annulus!